In 2004, Dean Oliver expanded upon his “Four Factors” philosophy from his 2002 book, Basketball on Paper, in an attempt to identify how four important strategies relate to success in basketball. These strategies are nothing new, as these were drilled into my head from coaches dating back to the early 90’s. The novelty of understanding these factors appear in the way of analytic development in an effort to shed light on emphasis of each factor.

In this article, we quickly walk through the four factors, illustrate their utility within the game; and then compare a statistical and a mathematical model to identify the relationship between success and the four factors of the game.

Four Factors: Score, Protect, Crash, and Attack

The four factors are to score efficiently, protect the basketball on offense, grab as many rebounds as possible, and get to the foul line as often as possible. Each of these elements are closely related to the termination of a possession for a team. There are other options such as dead ball rebounds, end of period, and specialized fouling situations. These are few and far between and rarely impact possession data over the course of a season. Hence we will focus on the main four ways to terminate a possession.

1. Score Every Possession.

This rule is the simplest of all and tends to be one of the hardest. An ideal team will always score, every time. However, teams are never ideal and we are left with attempting to identify the best way to measure scoring in the NBA. Oliver proposed using effective Field Goal Percentage (eFG%). This measure is a scale corrected measure to identify field goal percentage for a team. The scale correction is to account for three point field goals. Note, however, eFG% cannot be taken alone. For instance, you cannot determine the type of team (block vs. perimeter) with eFG% alone. However, with eFG% we do obtain the best relative measurement for points per field goal attempt; simple by multiplying by two.

To be clear, eFG% is given by

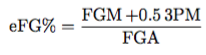
2. Pick Up All Rebounds

If a team cannot score on every possession, then the optimal task is to grab every miss and give the team a second-chance opportunity. An offensive rebound extends a possession and allows for a second attempt at a field goal. This is effectively a “do-over” for teams and when strategized around properly, can be a deadly plan of attack for a team.

To measure the quality of a team’s ability to rebound, we simply compute the offensive rebounding percentage (OREB%). This quantity is calculated as the number of offensive rebounds divided by the number of available rebounds after a missed field goal attempt. Note that this value is not over the number of missed field goal attempts.

The Toronto Raptors in the 2017 NBA season managed 871 offensive rebounds while giving up 2,619 defensive rebounds. Despite this, the Raptors missed 3,707 field goal attempts. This leaves 217 missed field goal attempts out of the picture. These can be attributed to dead ball rebounds, fouls before a rebound is secured, and expiration of period. Whichever reason, this is why we do not divide by the number of field goal misses. For the Raptors, their OREB% for the 2017 season is 0.24957.

3. Get to the Foul Line

The next way to score points other than scoring a field goal or giving the team a second opportunity is to get to the foul line. Getting to the foul line serves two purposes in a game. First, it guarantees attempts to score points. Second, it inches opponents ever closer to being out of the game. Just getting to the line is not enough. Converting said attempts into points becomes the most important part of the equation.

To measure a team’s quality of getting to the foul line is to identify the number of free throws made per field goal attempt, called the free throw rate (FTRate). The reason the comparison is to FGA instead of Number of Possessions is unknown. However, it’s not absurd. This is due to the fact that most teams average just under a field goal attempt per possession. For the 2017 NBA season, the worst team was the Brooklyn Nets (0.8401) while the best team was the Detroit Pistons (0.9414).

4. Protect the Basketball

The final step of the four factors is to ensure that, other than a defensive rebound, a field goal attempt or free throw attempt terminates the possession. That is, don’t turn the ball over. This is a simple measurement called turnover percentage (TO%). This measure is simply to calculate the percentage of possessions that ended in a turnover.

Four Factors? I Mean Eight…

Despite Oliver coining the term “Four Factors,” this process is actually eight factors. A team who scores a lot is not necessarily better. They have to stop their opponent from scoring. Ask Paul Westhead about that. This means that we can take the same four factors and calculate the opponent version for each team.

The lone exception is rebounding.

For rebounds, we instead calculate the defensive rebounding percentage (DREB%), which is the number of defensive rebounds divided by the number of opponent’s field goal misses that are available for rebound. Continuing on from the example above with the Toronto Raptors, who has a 0.24957 offensive rebounding percentage, we find that the Raptors grabbed 2,676 defensive rebounds while yielding 831 offensive rebounds. This results in a 0.76305 DREB% for the 2017 NBA season.

This means that we look at eight overall factors in Oliver’s Four Factors:

• Offensive Factors
  • Effective Field Goal Percentage
  • Turnover Percentage
  • Offensive Rebound Percentage
  • Free Throw Rate
• Defensive Factors
  • Opponent’s Effective Field Goal Percentage
  • Opponent’s Turnover Percentage
  • Defensive Rebound Percentage
  • Opponent’s Free Throw Rate

Here are the resulting four factors for the 2017 NBA season:

Measuring Impact on Success

In basketball, success is not the number of points scored, but rather the sign of the differential of score at the end of a game; called a win if the sign is positive. Hence success is defined as winning a game.

Oliver placed a certain set of weights on each of the four categories to ascertain value of each factor in regards to a win. The weights are

• 40% on Shooting
• 25% on Turnovers
• 20% on Rebounding
• 15% on Free Throw Rate

The question is whether these rates actually capture the winning tendencies of a team.

Model Fitting

To start, we can fit a naive model to the data above. Armed with the eight factors measured from 2017 data, we can use the number of wins as a response and perform a simple least-square s fit. This is a projective method that finds the hyperplane passing through the 8-dimensional “plane” (eight factors) passing through the 9-dimensional space (eight factors plus number of wins) such that the Euclidean distance between the plane and the observed number of wins is minimized.

If the data were assumed to be of Gaussian nature with fixed, independently, identically distributed errors, then we obtain the classical linear regression model. We ascertain the strength of fit by checking the residual sum of squares through the coefficient of determination. This measure identifies the percentage of variation between wins explained by the linear model. If this number is close to one, we have an explanation of the model to the data. In absence of statistical assumptions, this is fine. However, predictive power is not the greatest unless statistical assumptions are upheld. That is, take the results as a look into the past without using the weights to predict the future; unless assumptions are satisfied.

Model 1: No Intercept

If we proceed with no intercept, we assume that the model

The values of the beta’s are the weights associated to the number of wins out of 82 games. Note that this is just purely a mathematical model with no assumption checks. That said, applying a least squares fit through projective algebra, we obtain

• Beta 1: 351.1146
• Beta 2: -287.2934
• Beta 3: 137.1432
• Beta 4: 41.0642
• Beta 5: -409.9348
• Beta 6: 289.4278
• Beta 7: 58.7066
• Beta 8: -70.4028

So the results give us some pretty good feelings! First, the coefficients are in the correct directions! This means for every positive action a team makes, they are rewarded while every negative action a team makes is punished.

Second, the residual sum of square fit is high. This means that the coefficient of determination is indeed close to one! How close? The value is 0.9138. That’s a really decent fit.

Third, we obtain the model weights and therefore the weighting for each team!

Taking a closer look at the statistical model, we actually find that points scored drive teams to winning. This is relieving, but also quite uninformative.

We also find that Free Throw Rates are fairly negligible; as well as defensive rebounding. What this does show is that offensive rebounding and limiting turnovers are key to improving chances of winning.

An interesting note here is that defensive rebounding is valued less than offensive rebounding; which agrees with Hollinger’s PER model.

So what about these weightings? If we were to average their absolute values for each of the four factors, we gain insight into whether the 40/25/20/15 rule is upheld by the data. In this case we find:

• Shooting: 380.52 average
• Turnovers: 288.36 average
• Rebounding: 97.9235 average
• Free Throws: 55.7335 average

This yields a weighting of 46.2617 / 35.0574 / 11.9051 / 6.7758 result. This identifies that rebounding percentages and free throw rates are over-inflated and instead should have more emphasis on effective field goal percentage and turnovers.

To give full comparison, if we used the shoddy possession estimator formula of FGA + 0.44*FTA + TO we obtain weights of 44.8673 / 38.6925 / 9.8396 / 6.6006.

If we predicted the number of wins on the season using the linear model, we obtain a decent fit of 0.9138 and manage to adequately predict the number of wins with zero teams more than two standard deviations away from truth.

The worst predicted team is the New York Knicks: Predicted 37.5732 wins, Actual 31 wins. The other three far-tailed teams are the Miami Heat (Predicted 47.1967, Actual 41), Oklahoma City Thunder (Predicted 40.9732, Actual 47), and Boston Celtics (Predicted 47.0093, Actual 53). All other teams were within 4.5 games.

Model 2: With Intercept

If we enforce an intercept, we obtain a slightly better fit… as we are introducing a new variable into the model; however the improvement is negligible.

The p-value for this model indicates that the slope is negligible, however the model does indeed improve. So let’s naively keep this model and see what happens.

First off, the coefficients elicit similar weighting structure as the no-intercept model with a 44.5990 / 34.1605 / 15.5112 / 5.7293 as the weights. Again, turnovers are valued much more than Oliver pointed out previously. Also, again, free throws are less valued.

If we use this model to predict the number of wins, we obtain a slightly better fit overall; however the worst scenario is worse.

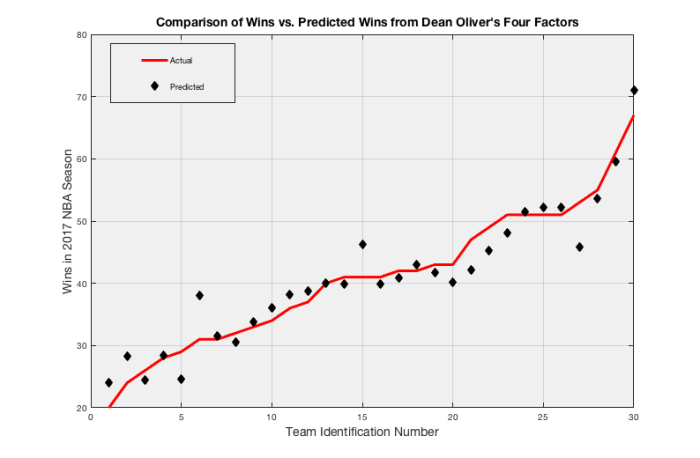
The worst case scenarios are again the Boston Celtics (Predicted 45.8309, Actual 53) and New York Knicks (Predicted 38.0212, Actual 31). However, Miami Heat and Oklahoma City Thunder tightened in closer to their prediction.

 

Principal Component Analysis Decomposition

To perform one last check , we take a cursory look at a principal component decomposition of the four factors matrix. In the previous exercises, we identified that free throw rates are fairly negligible with relatively high p-values; similar for defensive rebounds. Since we made the claim (without checking!) that the data is close enough to follow a Gaussian distribution, we may as well perform a PCA decomposition to look at some relationships between the factors.

To start, a principal component analysis (PCA) is a method that transforms the data from a Euclidean domain to an uncorrelated domain best ellipsoidal fit. The semi-major and semi-minor axes of the ellipsoid turn out to be the eigenvalues of the decomposition and give insight into the relationships of the data. For instance, if we find that two features are completely correlated, we will find that there is a zero eigenvalue.

Performing such a decomposition here, we find that the scaled eigenvalues for Oliver’s Four Factor analytic for the 2017 NBA season are 0.3030, 0.2229, 0.1916, 0.0990, 0.0732, 0.0515, 0.0333, and 0.0255. We scaled by the sum of the eigenvalues to give an idea of how much variance is explained by that axis of the ellipsoid. This direction/axis is called a principal component.

In this case, we find that 95% of the total variation in in Oliver’s Four Factors are explained by six principal components of the eight features. In fact, let’s keep seven components and run a regression on these components. We obtain the following results

We actually obtain a great fit in the reduced space (0.917 compared to 0.922). We can plug in the principal components into this model to obtain the weights for each of the four factors. The results look better intuitively, however note that this model is not better than the two linear regression models.

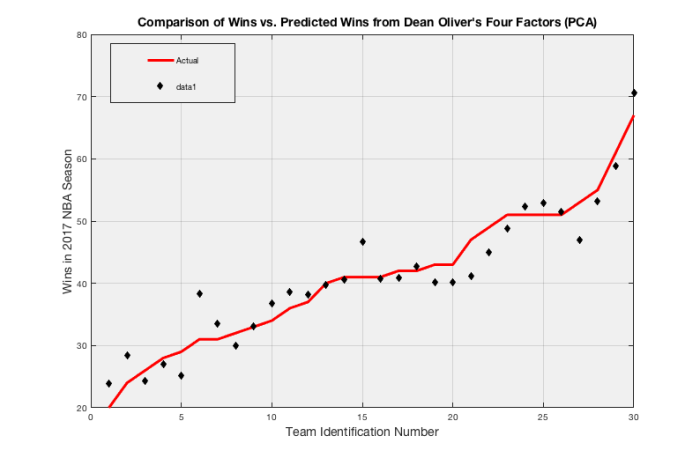
Again, the New York Knicks are near two standard deviations off with 38.2860 predicted wins compared to 31 actual wins. Similarly, the Boston Celtics are predicted to have 46.8997 wins compared to 53 actual wins.

What this model shows us is that Oliver’s four factors are indeed correlated; enough to reduce the dimensionality from 8 factors to 7. Unfortunately, the correlation is quite tangled and this does not indicate throwing out a particular factor.

 

Conclusions: Gaining the Edge

What Oliver’s Four Factors shows us is that an intuitive breakdown of a possession allows us insight on how to quantify the impact of possession completion on wins. For instance, finding a particular balance of rebounding, scoring, ball handling, and attacking of the rim is necessary in picking up wins in the NBA.

Finding the right mixture is pertinent as scoring and ball control are by far the strongest factors. However, isolating these variables is not the right way to go. Rather, this is an initial first step to identify weaknesses in a team’s ability to win. This give insight as to which of the four core areas a team is deficient compared to the league. From here, development of metrics to acquire talent to fill the necessary roles may be used, or even pure old school scouting and coaching to identify the non-measurable qualities of a player in an effort to improve players in current roles can be performed.

But the idea is simple: Score when you can; rebound for second chances when you can’t, and, according to my college coach… “Don’t ever turn the got damn ball over.”