In a recent podcast by Sixers Science, an analytic called the Kidd Score was unveiled. The goal of the analytic is to identify players who are great at two ancillary tasks: assists and rebounds. These two components are part of the big three statistical categories that make up the traditional triple double: points, rebounds, assists. If we consider the different ways a possessions ends, assists and rebounds are two of the primary causes. The other ways a player terminates a possession? Unassisted points scored and turnovers.  While scoring wins games, this statistic focuses on situations that either leads to points, or takes potential points away from opposing teams. In this post, we walk through Kidd Score, identify how this statistic works, note how it’s part of a subclass of NBA analytics called cross-product analytics, and then see what this statistic really tells us.

What is Kidd Score?

Kidd Score, named after Jason Kidd, takes a player’s assists per 75 possessions, a, and rebounds per 75 possessions, r,  over the course of a season and creates the square root of the multiple:

To understand this analytic, let’s test out a few players.

LeBron James (Cleveland): 8.5874

LeBron James played in a total of 74 NBA games in the 2017 season and amassed 646 assists and 639 rebounds. Scaled to 100 possessions, according to stats.nba.com, James’ per 75 possessions translates his totals to 8.625 assists and 8.55 rebounds. James’ associated Kidd Score is then 8.5874.

Russell Westbrook (Oklahoma City): 11.1740

Russell Westbrook became the first player since Oscar Robertson to record an average triple double in a season; roughly forty years after Robertson had achieved that feat. Westbrook managed to dole out 840 assists while nabbing 864 rebounds over the course of 81 games in 2017. This translates to 11.025 assists and 11.325 rebounds per 75 possessions, resulting in a Kidd Score of 11.1740.

Demetrius Jackson (Boston): 7.6101

Demetrius Jackson, as opposed to Westbrook and James, is a limited time (LT) player for the Boston Celtics, who managed to play in 17 minutes across five games in the 2017 NBA season. During his small amount of time, Jackson managed to pick up 3 assists and 4 rebounds; which is solid for a rookie seeing only 17 minutes of action. Due to this, his per 75 possessions stats are fairly strong, resulting in 6.6 assists and 8.775 rebounds. This results in a Kidd Score of 7.6101.

While these three players are different with respect to usage rates and time played, they have one distinguishing characteristic in common: they rebound at roughly the same rate as they pick up assists. So let’s look at two players who don’t share that trait.

DeAndre Jordan (Los Angeles Clippers): 4.8158

DeAndre Jordan is considered one of the best rebounders in the league. During the 2017 NBA season, Jordan grabbed 1,114 rebounds over 81 games. However, Jordan was not known for dishing out of the post; only managing 96 assists. This translates to 16.275 rebounds and 1.425 assists per 75 possessions. This results in a Kidd Score of 4.8158.

Ricky Rubio (Minnesota): 7.0436

Ricky Rubio, currently of the Utah Jazz, posted 682 assists and 305 rebounds over 75 games for the Minnesota Timberwolves in the 2017 NBA season. This translates to 10.5 assists and 4.725 rebounds per 75 possessions, resulting in a Kidd Score of 7.0436.

So we see how this score works and interacts with all types of players. So let’s take a deeper look into what this statistic is doing.

Cross-Product Statistics

If you listened to the Sixers Science podcast on Kidd Score, you would have noticed that the word metric was bandied about. Before we begin, let’s lay down terminology to understand what the Kidd Score is doing.

Common Definitions: Statistic, Analytic, Metric

A statistic is a function of data. That’s it. Simple. A statistic can be meaningful or it can be absolute garbage. Regardless, a statistic is merely a function of the data. An analytic is an algorithm that applies algebra or calculus to obtain a result. Typically an analytic is developed to provide insight, but an analytic is merely an algorithmic framework. Analytics and statistics almost go hand-in-hand, as statistics are frequently the output of an analytic.

A metric, on the other hand, is a standard of measurement. This inherently identifies that a measurement can be made; which is a loaded statement as measurements need to be consistent. That is, the distance between a point and itself better be zero. Similarly, the distance between two points are the same regardless of the direction we measure. And most importantly, the shortest distance between two points is a straight line. Note that straight line is defined with respect to the space of which we measure. Euclidean space is indeed a straight line, we all know and love; Spherical space straight lines are great circles.

Is Kidd Score a Metric?

In an exercise in testing if an analytic is a metric, we just have to check the three requirements of being a metric: non-negativity / identity, symmetry, and the triangle inequality.

Obviously, Kidd Score is non-negative as assists and rebounds are non-negative. The product of two non-negative values is non-negative. And, finally, the square root of a non-negative number is non-negative.

Now note, that this “measurement” is effectively measuring the distance from zero by definition. As the farther away from zero a player is, the higher the Kidd Score. In fact, a Kidd Score of zero indicates that the player must have 0 assists and 0 rebounds. This shows that non-negativity / identity are satisfied.

Next, we look at symmetry. Here, we must swap the distance from (0,0),  that is no assists, no rebounds, with the actual per 75 possession totals. This will give us negative distances within the square root; but since multiplication is being applied, the negatives cancel out and symmetry is indeed upheld. Mathematically speaking, we have

Finally, we check the triangle inequality. This asks if we can find a point in space that re-routes the metric in such a way that distance is minimized. In this case, we see the following:

This is very promising as we obtain the parts we need for seeing that Kidd Score satisfies the triangle inequality, with two extra hopefully non-zero terms. And this indeed satisfies the triangle inequality if and only if a player always has more rebounds AND assists then their comparison. Unfortunately, in the examples above, we see this is not true.

Therefore, Kidd Score is not a metric. Which is totally OK, because that means it’s a statistic. And it’s not only just a statistic, but it’s from a class of statistics called cross-product statistics.

Cross-Product Statistics

To understand the concept of a cross-product statistic, we first look at the definition of cross-product. The cross-product is a mathematical operation that helps us identify the area of a parallelogram spanned by two vectors. What this means is, is two vectors are orthogonal in two-dimensional space, then the cross-product looks for the area of the rectangle. In this case, for self-containment, orthogonal means that the two vectors meet at a right angle.

Now, if the two vectors do not meet at a right angle, then we get a diamond shaped image (parallelogram). The cross product still finds the area of this parallelogram, but it requires knowledge of the angle between the two vectors. This angle, describes the amount of correlation between the two vectors!! This means, that the cosine of the angle captures the correlation between two variables within the statistic.

To compute a cross-product, we adhere to some simple calculus. We consider the two vectors as being embedded in three-dimensional space: a = (a1, a2, a3) and r = (r1, r2, r3). We then form the determinant:

Now, if we consider assists and rebounds, these are effectively two vectors that we can write in the following manner: a = (a1, 0, 0) and r = (0, r2, 0). The way we think of this is assists run along the x-axis and rebounds run along the y-axis. If we ensure that the two variables are orthogonal, then we can apply this statistical framework. We will look into this in a moment. For now, assume these are orthogonal.

Plugging in the assist and rebound vectors into the cross product, we obtain

 

Which is merely the product of the number of assists and the number of rebounds! The value k tells us that we are projecting the product along the normal vector to assists and rebounds. We have effectively recovered the Kidd Score. Applying a square root to a set of positive numbers is a 1-to-1 transformation and is only necessary to make the numbers look to be the same scale as the original variables of assists and rebounds. But that’s another story.

In fact, another formulation for the cross-product is given by

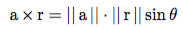
That is, the cross product is the magnitude of the first vector, times the magnitude of the second vector, multiplied by the anti-correlation between the two vectors. Since we assumed rebounds and assists to be orthogonal, theta is 90 degrees and therefore the sine is one; whereas the cosine (amount of correlation) is zero.

So let’s actually look into this correlation thing…

Relationship of Assists and Rebounds: 2017

A quick way to look into the relationship between assists and rebounds for the 2017 NBA season is to look at the scatter plot. From these, we can compute the sample correlation and perform a simple statistical test.

We see that there is some sort of skew between obtaining assists and obtaining rebounds; that somewhat indicates the more assists a player gets, the less likely they are to obtain rebounds.However, on our plot, please note that the x-axis is not at the same scale as it runs up to 12, while the y-axis (rebounds) runs up to 20. Regardless, we see there is a downward trend as the upper quarter quadrant is sparse with players.

To be sure, we can compute a correlation test to identify if we do indeed have correlation between assists and rebounds. In forming this statistic, we should at least address one hidden elephant in the room. Danuel House (Washington) tops the list of rebounders at 49.3 rebounds per 75 possessions. This is due in part to playing one minute of action and picking up one rebound. We will take a look at correlation with and without House just to show his effect on the distribution of this statistic.

Testing Correlation: Pearson’s t-Test

The simple test for correlation is the Pearson t-Test. Computing the correlation for the entire 2017 NBA season, we obtain a correlation coefficient of -0.3207. This suggests the downward trend that we notice, however is this within variation of the values zero?

The Pearson t-Test for correlation is a statistic that captures the distribution of the standardized correlation statistic centered at zero. Therefore, any correlation that falls to the tails of the statistic’s distribution will be seen as a low-probability event and therefore identified as not being from the distribution of a zero-centered correlation. This in turn states that the observed correlation is significant.

The formula for the standardized correlation statistic is given by

where t is the test statistic, n is the number of players observed, and r is the sample correlation. In this case, we obtain a test statistic of t = -7.2287. This has a small p-value of 2.247×10^(-12). Indicating that there is indeed a downward trend.

So let’s remove House and see what happens. It turns out that deleting house actually decreases the correlation, making it -0.3208. This indicates that House barely has any effect on the correlation; despite being an outlier.

What this test has shown is that assists and rebounds are not orthogonal and therefore the Kidd Score biases players in the direction of information loss. We will touch on information loss in a moment.

Correcting Kidd Score to Reflect the Assist – Rebound Relationship

The geometric interpretation of correlation is that it is the cosine of the angle in-between two variables. In fact, those familiar with Principal Component Analysis (PCA) understand how to transform the data with high correlations into orthogonal variables; which in fact builds off the notion of cosine similarity between variables of interest by correcting through an eigenvector decomposition. (There’s much more to this, but out of the scope of this article).

Therefore the cross product statistic, such as Kidd Score, should look into incorporating the assist-rebound relationship through the anti-correlation term, sine theta. Note that this term is exactly in the denominator of the Pearson t-Test!!! This is seen as:

In this case, we have r = -0.3207, which yields a multiplier of 0.9472. This indicates that assists and rebounds, while proven to not be orthogonal, are near-orthogonal. As we have a negative cosine term and a positive sine term, we obtain a negative tangent term, which is the Pearson t-Test ratio; not including the n-2 term. For a negative tangent value, since assists are the reference axis (cosine here dictates direction of assists) and assists are seen as negative valued, then the Kidd Score biases in the direction of assists; as they are effectively absorbing roughly 4% of rebounds, according to the anti-correlation statistic.

The simple correction? Compute

In this case, we see the according adjustments for the 2017 NBA season:

• LeBron James: 8.5874 -> 8.1338
• Russell Westbrook: 11.1740 -> 10.5838
• Demetrius Jackson: 7.6101 -> 7.2082
• DeAndre Jordan: 4.8158 -> 4.5614
• Ricky Rubio:  7.0436 -> 6.6716

This adjustment correct for the correlation seen within the NBA season and allows us to compare across seasons.

At this point, there’s still an issue with using rates, as Demetrius Jackson currently sits in “HoF’er territory.” The common practice to set a threshold and say “minimum number of possessions required.” However, as scaling through number of possessions may help rectify this. However, sitting at 2000+ words, I’ve already hit the goal of showing how to break out a cross-product statistic and build it with respect to the geometry of the analytic methodology imposed on the data.

If you haven’t checked it out already, I encourage you to check out their podcast: located here. The statistic captures many hall of fame players at the raw level and they use it in attempts to predict seasons for players such as Ben Simmons. It’s a neat little intuitive statistic that captures two integral parts of the game and players that rate high have a tendency to take away possessions from teams while increasing their teams point totals without having to score themselves.