In a fairly comical article back in February 2018, Bleacher Report identified the League’s Least Valuable Shooters. In this article, Adam Fromal examined players around the league by extracting their field goal percentage from four particular zones on the court: 3-10 feet, 11-16 feet, 17′-3pt, and 3PA. Fromal would then calculate each player’s points per shot from each zone and multiply it by their number of attempts; thus giving us a look at the points generated. Form there, Fromal would compare this to the league average (normalized to the player’s attempt rate) and take the difference. The result would identify the amount of value added over average by the player’s shot selection and quantity. Let’s take a quick look at three examples.
James Harden
Since we are in the middle of a historic run, let’s take a look at James Harden of the Houston Rockets. According to Basketball Reference, Harden is 58-143 from between 3-and-10 feet, 22-42 from between 10-and-16 feet, 6-20 from long-range two’s, and 218-583 from beyond the arc. This leads Harden to have a sample expectation of 1.0482 points per FGA. Recall that we come to this number by computing the effective Field Goal percentage over the regions of interest and multiplying this number by two.
In comparison to the league, through January 25th, there has been a total of 13,246 FGA. Of these 13,246 FGA, the league has taken 37,174 between 3-10 feet; converting 14,817 of them. Similarly, the league is 8491-for-20,731 from 10-16 feet, 4942-for-12,321 from 16-to-3pt, and 15,963-for-45,015 from three-point range. This leads to a league average of 0.9058 points per non-rim FGA.
Hitting Harden’s 788 non-rim attempts from the field, we see that Harden is a whopping +112.2112 points over league average on shooting attempts.
Russell Westbrook
If we compare Harden to his MVP “nemesis” Russell Westbrook, we find that Westbrook’s numbers are 10-for-63 from 3-10 feet, 41-for-130 from 10-16 feet, 47-for-123 from 16′-to-3pt, and 46-for-189 from three-point range. This leads to an estimated expected 0.6614 points per non-rim FGA. Yikes. This leads to a -123.43 points over league average. Pay attention to the negative in that statement. Read that as Westbrook is one of the most detrimental “shooters” in the league. This is consistent with Fromal’s analysis last season as Westbrook was second on the list for the 2017-18 NBA season.
Klay Thompson
If we turn to Klay Thompson, we find an entirely different story. This season, Thompson has a shot distribution of 25-for-63 from 3-10 feet, 58-for-134 from 10-16 feet, 104-for-218 from 16′-3pt, and 138-for-363 from beyond the arc. This leads to an estimated expected 1.0129 points per non-rim FGA. Comparing Thompson’s efficiency and volume relative to the average shooter in the league, and we find that Thompson is much like Harden in picking up a +83.2876 points over league average.
Note that we focus on volume of shots to separate out shooters from non-shooters who happened to have luck on their side.
Rumblings about Stephen…
And before we continue, we selected Klay Thompson instead of Stephen Curry for a very specific reason. For those who may be interested, Stephen Curry leads the league in points per non-rim attempt (at high volume) with a phenomenal 1.2187 points per non-rim FGA. This leads to a yet-again league leading +197.4402 points over league average when considering his volume.
Why These Three Guys?
Given the three players above: James, Russ, and Klay, we have identified three different types of shooters:
Harden is the playmaking scorer-shooter combo. This type of player generates their own points and can tear apart a team from long range. This is the deadliest type of player in the league. Defenses have to make conscious decisions on whether to guard the drive, guard the pullup/stepback, whether to blitz/double and leave another shooter potentially open, or have to leave the shooter in off-ball situations in help defense.
If we think of the scorer-shooter combo, there are three levels of this player despite doing both. Harden is a SCORER-shooter while Curry, mentioned above, is more of a scorer-SHOOTER. Something we will touch on later.
Westbrook is the playmaking scorer. Westbrook is a high-usage player due to his ability to get to the rim and collapse defenses. Not known for his shooting touch, Westbrook shoots just enough, call it “Marcus Smart enough”, to make defenses think twice before giving him space at the perimeter. Westbrook generates offense more through his scoring abilities but will tend to lose games if forced to take all the big shots outside of 3-feet. Hence the reason for Paul George’s over-the-top strong emergence this season; reminding us of the Indiana days of PG13.
Klay Thompson is the shooter. This type of player is a pure shooter than can pick apart a team at any time they want. Sure, Thompson can generate points on his own, but he’s best utilized as an off-the-ball catch-and-shoot monster that can put up 20-30 points in a hurry. He is the perfect complement to a playmaker such as Stephen Curry or Russell Westbrook.
Side Note: If you are unsure of the difference between a shooter and scorer, feel free to have a discussion in the comments. This is a very important distinction that is made when discussing players around the league (and has been for well over a decade).
Now suppose we are interested in evaluating three players that are respective teammates to Russell Westbrook, James Harden, and Klay Thompson. Suppose these players are considered equivalent defensive players. And furthermore, to constrain the problem, suppose they play the same number of possessions as each other with their respective teammates, playing identical opponents, and have identical net ratings.
We’d like to ask, which of these three smaller-fish players are more important to their offenses? And it’s here where the “missing-ness” of stats rears its ugly head. This one being the missed FGA off a pass, also known as the potential assist.
Potential Assist: What Could Have Been…
A potential assist is a situation where a ball-handler make a pass to a player who takes a field goal attempt within the determined amount of time an effort required of earning an assist, called an assist window, if the field goal is converted. Tracking assists is easy. When a field goal is made the play-by-play logs tack down who the passer was, if there was a passer within the assist window. However, when a field goal is missed, the assist field is zeroed out as no assist was made. Tracking these assists are relatively easy, it just isn’t done.
Instead, we are forced to look at other methods for determining a potential assist. For instance, we can look at tracking data and surmise a filtering algorithm akin to extracting passes. But for assists does that actually work? Let’s look at what the league has to say about passes:
An assist is a pass that directly leads to a basket. This can be a pass to the low post that leads to a direct score, a long pass for a layup, a fast break pass to a teammate for a layup, and/or a pass that results in an open perimeter shot for a teammate. In basketball, an assist is awarded only if, in the judgement of the statistician, the last player’s pass contributed directly to a made basket. An assist can be awarded for a basket scored after the ball has been dribbled if the player’s pass led to the field goal being made.
Therefore, unlike passes, there is no distinct rule-based definition on what constitutes an assist. it is literally defined as a subjective statistic, which can be defined differently across different teams. Therefore, we cannot easily place a rule-based mechanism like we did in the past for passes, after all. Instead, we turn to the work of machine learning.
Ultimately, we need to know whether passing to James Harden, Russell Westbrook, or Klay Thompson is going to improve a teammate’s chances of receiving a reward such as an assist for a made basket or a bump in points produced and therefore increasing their offensive rating. By looking at the hard numbers above, if we all wanted to pad our stats then we’d all want to be Klay Thompson’s or James Harden’s teammate. Or do we?
Building a Potential Assist Model
In an effort to build a potential assist model, let’s apply a supervised learning technique to help introduce labels and training into our system. Fortunately, we have a sample of labels already gathered for us through the play-by-play assist. To start, we can walk through every made field goal attempt and split them into two classes: assisted field goals and un-assisted field goals. Using a “0/1” label as our response variable we can employ some sort of model to identify the differences between certain explanatory variables such as dribbles taken, feet traveled, seconds between pass and shot, etc. in an effort to understand if a player takes two dribbles after receiving a pass could the passer be credited with an assist.
Immediately, to the novice user, a logistic regression model comes to mind since the response is binary. However, one issue that arises with logistic regression, is that we must assume that the log-odds ratio is conditionally linear with zero multicollinearity across all the explanatory variables. More importantly, this conditional model must satisfy the exponential family assumptions in the log-odds space, which, unfortunately, usually ultimately fails in basketball analytics.
Next, we could leverage a neural network to do our dirty work for us. And indeed we could. However, we have a better idea for teaching some neural networks in a future posting, and why not go crazy in learning something entirely different…
Support Vector Machines
A fairly flexible methodology in classification is the support vector machine (SVM). In practice, this is called a separating hyperspace algorithm that aims to take the explanatory variables and split the classes using hyper-planes until all classes are split into uniform regions. Let’s look at a really basic example.
Suppose we sample 1000 points within the unit square with a decision boundary decided by some 5th-order polynomial. Anything below the polynomial is considered class 1 while anything above the polynomial is considered class 2. Given the 1,000 samples, we can easily see the boundary:

1000 samples from a simple classification problem. Can you see the boundary between the blue and green classes?
To show we’re not hiding any cards up our sleeves, here’s the plotted decision boundary. between the two classes:
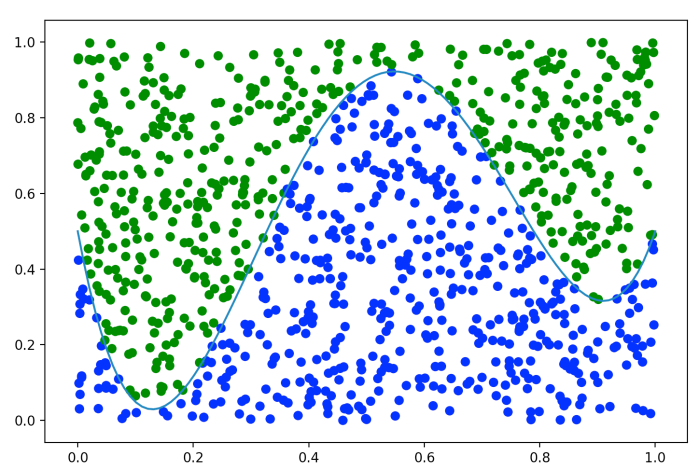
Decision boundary included!
And you can even try this at home:
<code>
import numpy as np
import random</code></pre>
x = [[],[]]
y = np.array([])
cols = []
for i in range(1000):
p = random.random()
q = random.random()
boundary = .5-(124./15.)*p + 44.*p*p - (1016./15.)*p*p*p + 32.*p*p*p*p
if q < boundary:
y = np.append(y,0)
cols.append('blue')
else:
y = np.append(y,1)
cols.append('green')
x[0].append(p)
x[1].append(q)
dots = np.linspace(0,1,100)
bounds = np.zeros(100)
for i in range(100):
p = dots[i]
bounds[i] = .5-(124./15.)*p + 44.*p*p - (1016./15.)*p*p*p + 32.*p*p*p*p
plt.plot(dots, bounds)
plt.scatter(x[0],x[1],c=cols)
plt.show()<code>
Now, if we apply a Logistic Regression, we obtain the following results:
X = np.array(x).transpose() clf = LogisticRegression(solver='lbfgs').fit(X,y) yhat = clf.predict(X)
And we find that we have a success rate of approximately 75% of correctly classifying the points! That’s actually not too good given we can easily see the boundary. This terrible results comes from the fact that this particular boundary problem and associated distribution requires a curved exponential family to improve on its boundary. That is, we’d have to develop a weighting scheme in order to satisfy the assumptions of the logistic regression. In two-dimensions, this is rather straightforward. However in multiple dimensions, we get into a lot of trouble as we cannot view the results.
A support vector machine will look for a collection of separating hyperspaces to partition the two classes. In the two-dimensional case, we will identify segments of straight lines that partition the data. If we assume a linear boundary, this will give us the best fitting “linear model”:

The yellow region is the “best hyper-space” separating two classes. The image on the right identifies measuring errors when two classes are “mixed.” (Image from Elements of Statistical Learning)
However, we don’t restrict ourselves to the linear model in SVM’s. We actually employ what are called kernels, which give weight to each data point. When paired with the potential separating hyperspace and the observed classification label (assist or non-assist), we obtain a “linear” boundary as such:
The image on the left shows the “Logistic Regression” type model with a linear discriminant. The image on the right shows the learned “linear boundary” from SVM’s. (Image from Elements of Statistical Learning)
If we apply this to our scheme, we find we obtain a much better classifier.
clf2 = svm.SVC(kernel='rbf',gamma=10) clf2.fit(X,y) yhat2 = clf2.predict(X)
Here’s we applied a radial basis function as a kernel and settled on the value of 10, which is a smoothing parameter for the radial basis function. Selecting this parameter should be performed by cross-validation. In this case, the value of 10 from one-fold cross-validation gave us an average error of 0.03%. Much better than the 25% from logistic regression. And this was on well-separated data.
Onto Potential Assists!
Crediting an assist to a made field goal is not a well-separated distribution. There have been several instances where a play will be credited an assist for one player, but the same action may not be credited for another player. In these cases, this boils boil to the differences in judgement between two different crediting statisticians. Using the assist crediting for converted field goals, we can train an SVM model to identify key features for determining an assist when a FG is made.
Many of these features need to be teased out of tracking data, and unfortunately due to the exclusivity of the data, I cannot share code or even the data itself. However, if you get your hands on tracking data, you can test out some of these features. Note that in these results, we will use the notation of class zero being no assist on attempt and class one being assist on attempt. Here are the primary features that yielded great results
Feature 1: The Pass
Yes, this is an obvious one. Passes are highly correlated to assists. And due to this we can immediately set field goal attempts where there were no passes were made to class zero. This is a well-separating feature and is the by far the most dominant feature in determining assists.
Feature 2: Dribbles After Reception
The second feature that well-separates the classes is the number of dribbles. And it’s also this one that starts to make situations a little mixed in the results. In fact, this season, there has been a couple assists generated off of three or more dribbles after the pass. For the most part, it’s effectively one or zero dribbles. Due to this draw down, there’s some room for error in predicting an assist.
Feature 3: Seconds between Pass and FGA
We can also measure the amount of time between receiving a pass and taking a field goal attempt. The significant range lays within the first 1.5 seconds of a shooter receiving the ball. A lot can happen in 1.5 seconds of action. Despite this, we do find a significant bulk of assists lay (softly) around this boundary. This feature is the third most significant feature and actually gets tangled up with the above feature and next most significant feature.
Features 4 and 5: Velocity “Swing” of Shooter
Through film study, we notice that a player who “swings” their velocity impacts whether an assist gets credited. A “swing” in this case is when the player’s velocity vector swings from going along the axis of a FGA attempt into an entirely different direction. Just like a swing.
We use the axis notation as a player may be slowing in their direction towards the basket. And in fact, it’s not the player we measure, but rather the basketball. The example is given as a pass into the post. A player who catches the ball may be on the run, and hence their velocity vector is pointed at the basket.
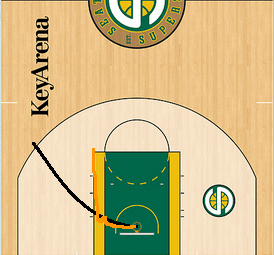
Lead pass from elbow and the ball jostles for the right hand layup. This is credited as an assist.
In the cases of a turn-around, the velocity vector will point away from the basket, but along the same arc. These tend to be credited as assists as well. However, if the player makes an extra move, then the assists may no longer be an assist. For example, a player may stop and pump fake. Or the player may perform a cross-over or spin move. It’s these points where the judgement begins to become mixed.
Despite the judgement, we see the velocity vector of the basketball start to become orthogonal to the direction of the basket, which indicates a basketball move is occurring and the assist is more than likely going to evaporate.
Therefore a velocity swing is the cosine angle of the player’s velocity vector towards the basket and the basketball’s cosine angle of the basketball’s velocity relative to the player’s velocity. Note that this value is always between 0 and 1. If we integrate the cosines over the time between reception and attempt (feature three) we obtain out total amount of velocity swing. Small values of these lead to assists.
Using these features and a leave-one-out cross-validation, we obtain a 98.77% recall rate of crediting an assist when a field goal attempt is made. Not too shabby! This means we will typically potentially mess up 1-3 shots per game as teams tend to shoot between 150 and 200 shots, combined over the course of that game. We can live with this as, after all, assists are subjective to being with.
Finally a Potential Assist
Now recall that we used actual assists to learn out SVM. Despite this, we never actually used the made field goal to train our data. Therefore, a missed field goal attempt suffers the same fate as a field goal attempt in the eyes of the assist. As a thought exercise, we show a creditor 100 “made field goals” and simply cut off the video before each ball was released, tell the creditor that “yeah, it was made anyways,” and we ask whether the play was credited as an assist. It then turns out all of these attempts were misses; it does not change the outcome of the experiment.
In this case, we apply the potential assists to all of our games that James Harden, Russell Westbrook, and Klay Thompson have played. Due to the availability of the data, we have only every game through January 16th of 2019. Despite this, we have the following results of our SVM:

Distribution of potential assisted FGA for Harden, Westbrook, and Thompson.
And immediately we see the differences between these three candidates; and the reason why we selected these three players.
Harden is a Creator
Immediately popping off the page is James Harden and his 7.57% of field goals being potentially assisted! That’s absurd. Furthermore, when he is potentially assisted, Harden posts an effective field goal percentage of 0.6094, which leads to an estimated expected 1.2188 points per FGA. Of course, the rim-attempts are tangled in here; so be cautious with the stats.
That said, we find that only 8.81% of Harden’s three point attempts are potentially assisted. Again, a counter-intuitive game plan according to the catch-and-shoot trends in the league. In fact, Harden’s 3P% in potentially assisted attempts is 37.2%, which is almost identical to his pullup and stepback three point game, which is at 37.5%.
What this suggests is that we should up-weight a teammate’s assist total when they work with a high-usage player like Harden due to the fact that Harden will make significant moves after receiving the ball. Being Harden’s teammate when it comes to measuring true passing vision as most passes will not end up in attempted shots. Therefore a simulation mechanism needs to be in place for ascertaining value of the pass.
Thompson is a Shooter
On the other end of the spectrum, Thompson is a passer’s best friend. Here we see that Thompson is fairly high up in percentage with 67.69% of all his FGA being potentially assisted. More staggeringly, over 90% of Thompson’s three-point attempts are potentially assisted. For all high volume shooters, this is the highest in the league (by far).
Much like Harden, Thompson’s efficiency barely changes depending on the three-point attempt; as he is a 37.8% shooter in potential assist situations and slightly over 38% in all other situations.
Westbrook requires a Potential Assist
Westbrook is the passing teammate’s nightmare; in the sense that an assist is not likely to get credited if Westbrook shoots the ball. Due to this, since Westbrook is an MVP caliber player capable of making plays and winning games, the teammate needs to make the pass. With this in mind, we can up-weight this player’s assists totals much like HArden’s teammates, as they are making the passes and just not getting the results. In Harden’s case it’s an extra action that’s taken. In Westbrook’s case it’s just bad luck.
As a note, Westbrook shoots 27% on potentially assisted three point attempts while dropping down to 23% on pullup and stepback attempts. In this case, we actually see a fairly significant improvement in percentages; regardless of the low percentage.
Moving On…
By leveraging a machine learning algorithm like a support vector machine, we are able to start developing models to help us understand difficult to measure quantities such as a potential assist. There are many more ideas we can pop out using this type of machine learning capability. For instance, a follow on question may be, can we use extra features to identify designs of plays in-game that will CREATE potential assists?
The short answer?
Yes.




Pingback: The Potential Assist
Pingback: Weekly Sports Analytics News Roundup - January 29th, 2019 - StatSheetStuffer