As Week 7 of the NFL season comes to a close, we have tallied a total of 119 of the 256 regular season football games. This equates to just over 46% of the season completed. In these seven weeks, we have four undefeated teams remaining: New England, Cincinnati, Denver, and Carolina. In a previous post, we used logistic regression to predict the final standings by yielding a power rankings. In that model, we assumed the output is given as a win or loss and we modeled the probability that a given team will win in a particular match-up.
In this article, we take a look at predicting the distribution of points relative to a win. Several models use a margin of victory by taking a diminishing returns model where close games are given higher weight than games that result in blow-outs. Instead of following this traditional model, let’s form the ratio of points scored by a team. That is, if the New England Patriots win a game 54 – 10, then the result of the game is not 1/0 (win/loss) but rather 0.84375. Here, the winning team has a score ratio above 0.5000. So we will instead model the score ratio and treat this as a probability that a given team will win.
Score Ratios Follow a Beta Distribution.
A score ratio is given by the formula
p = (Team A Points Scored) / (Points Scored In Game)
and can only be between 0 and 1. The score ratio for the opponent is merely 1-p. Similarly, a Beta Distribution models random variables between 0 and 1 by comparing the relationship between the value and its additive inverse. In layman terms, we model the distribution of p and 1-p.
In order to develop a beta regression model, we need to find a link function to transform the mean response, to a number between negative-infinity to infinity. We find that the logit link function that was used in logistic regression works well here, however we do not assume Gaussian error. Instead, we use the log-likelihood function of the beta distribution and write the average of the beta distribution as a function of the logit link function. There is some serious math going on here, and thanks to Silvia Ferrari and Francisco Cribari-Neto, we have a numerical solution for calculating this expectation.
Using the logit link function, we have a linear model where the coefficients give us a strength of points scored by a given team. The covariates used is the same set up as the logistic regression model where indicators are used for teams playing and home field. Using the beta regression model, we obtain the strengths of each team.
Using the rankings model, we are then able to run a Markov Chain Monte Carlo simulation to predict the final standings for the season.
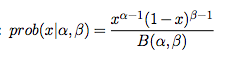


Pingback: NBA Power Rankings – November 8th | Squared Statistics: Analyzing Crime, Sports, and People